Astronomická jednotka
Astronomická jednotka (1 au) je definována jako střední vzdálenost středů Země a Slunce. 1 au je přibližně 150 milionů kilometrů (149 597 892 ± 5 km přesně).
Světelný rok
Světelný rok je vzdálenost, kterou urazí světlo za jeden rok ve vakuu:
1 ly = 299 792 456 m · s-1 · 365,25 dnů · 24 hodin · 60 minut · 60 sekund = 9,461 · 1012 km
Parsec
Parsec (1 pc) je vzdálenost hvězdy, jejíž roční paralaxa je 1“ (jedna úhlová vteřina).
Paralaxa p úhel, pod kterým z hvězdy vidíme nějakou definovanou délku, např. paralaxa rovníková je úhel, pod kterým bychom viděli průměr Země. Paralaxa roční \(\pi\) je úhel, pod kterým bychom z dané vzdálenosti viděli délku 1 au (viz obrázek).
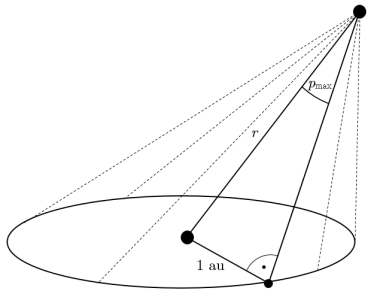
Paralaxa hvězdy se většinou měří tak, že se určí úhel, pod kterým vidíme tuto hvězdu vhledem ke vzdáleným hvězdám. Poté se tentýž úhel změří za půl roku a rozdíl se vydělí dvěma. Tato metoda však funguje jen pro blízké hvězdy.
Pokud známe roční paralaxu \(\pi\) hvězdy (změřenou podle obrázku), její vzdálenost \(r\) určíme jako
Zde \(r\) i \(\pi\) jsou ve složených závorkách, protože takováhle rovnice nesedí rozměrově; ve jmenovateli není funkce tangens, protože pokud budeme \(\pi\) dosazovat v radiánech, tak pro takto malé úhly je hodnota tangenty rovna přímo úhlu v radiánech a není potřeba do toho plést trigonometrické funkce).
Pro velikost jednoho parsecu platí: